[머신러닝] 회귀 모델

머신러닝&딥러닝

[머신러닝] 회귀 모델

s2h15 2023. 12. 21. 16:51

728x90

1. 회귀 모델 - KNN 회귀모델(KNeighborsRegressor)

농어 길이로 농어 무게를 예측해보자

데이터 : 농어길이 와 농어 무게 데이터

# 농어 길이
perch_length= np.array(
    [8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0,
     21.0, 21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5,
     22.5, 22.7, 23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5,
     27.3, 27.5, 27.5, 27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0,
     36.5, 36.0, 37.0, 37.0, 39.0, 39.0, 39.0, 40.0, 40.0, 40.0,
     40.0, 42.0, 43.0, 43.0, 43.5, 44.0]
)
# 농어 무게
perch_weight= np.array(
    [5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0,
     110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0,
     130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0,
     197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0,
     514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0,
     820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0,
     1000.0, 1000.0]
)

- 독립변수 : 길이

- 종속변수 : 무게(연속형)

-> 종속변수가 연속형이기에 회귀모델을 사용해야한다.

① 분포 확인 위한 산점도 그리기

import matplotlib.pyplot as plt
plt.scatter(perch_length , perch_weight)
plt.xlabel("length")
plt.ylabel("weight")
plt.show()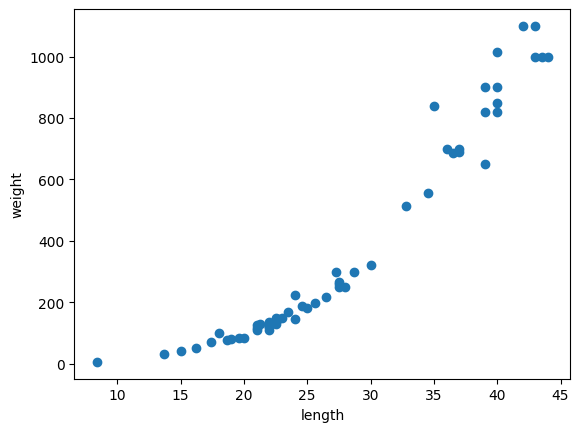

▶ 우상향 형태를 띄고 있다.

초반에는 약간의 곡선 형태를 띄는 듯 하다가 중후반 부터는 직선의 형태를 띄고 있다는 것을 확인할 수있다.

우상향 그래프로 농어의 길이가 길어지면 농어의 무게도 무거워지는 것을 알 수 있다.

② 훈련 및 테스트 데이터 분류하기

훈련 : 테스트 = 75:25 로 구분

사용변수 : train_input , train_target , test_input , test_target

from sklearn.model_selection import train_test_split
train_input,test_input,train_target,test_target = train_test_split(perch_length,perch_weight,test_size=0.25,random_state=42)
print(f"{train_input.shape}, {train_target.shape}/{test_input.shape} , {test_target.shape}")

(42,), (42,) / (14,) , (14,)

▶ 훈련 데이터 42행 , 테스트 데이터 14행

③ 훈련 및 테스트의 독립변수를 2차원으로 만들기

reshape(행 , 열) : 차원 또는 행 열 개수 변환 함수

-1은 전체를 의미함

train_input = train_input.reshape(-1,1)
test_input = test_input.reshape(-1,1)
train_input.shape , test_input.shape

((42, 1), (14, 1))

④ 모델 생성 & 훈련 & 정확도 확인

회귀 모델은 KNeighborsRegressor 를 import하여 클래스를 생성한다.

분류 모델에서는 정확도라고 하고 회귀에서는 결정계수(R^2) 라고 한다.

from sklearn.neighbors import KNeighborsRegressor
knr  = KNeighborsRegressor()
knr.fit(train_input,train_target)
train_r2 = knr.score(train_input,train_target)
test_r2 = knr.score(test_input,test_target)
train_r2,test_r2

(0.9698823289099254, 0.992809406101064)

▶ [해석]

- 훈련 및 테스트 정확도가 매우 높게 나타난 성능 좋은 모델로 판단됨

- 과적합 여부를 확인한 결과, 훈련 정확도 < 테스트 정확도 이므로 과소 적합이 발생하고 있는것으로 판단됨

- 이는 데이터의 개수가 작거나 튜닝이 필요한 경우

⑤ 모델 평가하기 : 평균 절대 오차(MAE)

< 평균 절대 오차(MAE , Mean Absolute Error ) >

- 회귀에서 사용하는 평가방법

- 예측값과 실제값의 거차이를 평균하여 계산한 값

- 즉, 사용된 이웃들과의 거리차를 절대값으로 평균한 값

○ 라이브러리 정의

from sklearn.metrics import mean_absolute_error

○ 예측하기

test_pred = knr.predict(test_input)
test_pred

[ 60. 79.6 248. 122. 136. 847. 311.4 183.4 847. 113. 1010. 60. 248. 248. ]

▶ 각각 14개의 테스트 독립변수에서 5개씩 이웃을 선정하였을때 그 다섯개의 이웃의 거리 평균값이 나온다.

즉 이것이 예측값이 된다.

○ 평가하기

mae = mean_absolute_error(test_target,test_pred)
mae

19.157142857142862

mean_absolute_error(실제값 , 예측값) -> 실제값 - 예측값의 평균치

▶ [해석]

- 해당 모델을 이용해서 예측을 할 경우에는 평균적으로 약 19.157g 정도의 차이(오차)가 있는 결과를 얻을 수 있음

- 즉, 예측결과는 약 19.157g 정도의 차이가 있음

⑥ 과소적합 해소하기 - 하이퍼파라메터 튜닝

KNN 모델의 이웃의 개수를 조정해보기

○ 이웃의 개수 기본값(5)일때

# 이웃의 개수 -> 기본값 사용
knr.n_neighbors = 5
# 하이퍼파라메터 값 수정 후 재훈련시켜서 검증해야한다.
knr.fit(train_input,train_target)
#훈련 정확도 확인
train_r2 = knr.score(train_input,train_target)
# 테스트(검증)정확도 확인
test_r2 = knr.score(test_input,test_target)
print(f"훈련 = {train_r2} / 테스트 = {test_r2}")

훈련 = 0.9698823289099254 / 테스트 = 0.992809406101064

▶ [해석]

- 과적합 여부 확인 결과 과소적합

○ 이웃의 개수 3으로 수정시

# 이웃의 개수 -> 기본값 사용
knr.n_neighbors = 3
# 하이퍼파라메터 값 수정 후 재훈련시켜서 검증해야한다.
knr.fit(train_input,train_target)
#훈련 정확도 확인
train_r2 = knr.score(train_input,train_target)
# 테스트(검증)정확도 확인
test_r2 = knr.score(test_input,test_target)
print(f"훈련 = {train_r2} / 테스트 = {test_r2}")

훈련 = 0.9804899950518966 / 테스트 = 0.9746459963987609

▶ [해석]

- 과소적합 해소를 위해 이웃의 개수를 조정하여 하이퍼파라메터 튜닝을 진행한 결과 과소적합을 해소할 수 있었음

- 또한 훈련정확도와 테스트 정확도의 차이가 크지 않기에 과대적합도 일어나지 않았음

- 다만 테스트 정확도는 다소 낮아진 반면 , 훈련 정확도가 높아졌음

- 이 모델은 과적합이 발생하지 않은 일반화된 모델로 사용가능

○ 최적의 이웃 개수 찾기

knr = KNeighborsRegressor()
knr.fit(train_input,train_target)
nCnt = 0
nScore = 0
for n in range(3,len(train_input),2):
 knr.n_neighbors = n
 score = knr.score(train_input,train_target)
 # print(f"{n} / {score}")
 # 1보다 작은 정확도인 경우
 if score < 1:
  # nScore의 값이 score보다 작은 경우 담기
  if nScore < score:
   nScore = score
   nCnt = n
print(f"nCnt = {nCnt}/ nScore = {nScore}")

nCnt = 3/ nScore = 0.9804899950518966

▶ 최적의 이웃개수는 3이라는 것을 알 수 있다.

⑦ 임의값으로 예측하기 & 이웃 개수 구하기 & 산점도 그리기

○ 길이 50으로 무게 예측하기

knr.predict([[50]])

1033.333333

○ 사용된 이웃의 인덱스 확인

dist , indexes = knr.kneighbors([[50]])
print(indexes)

[[34 8 14]]

○ 산점도 그리기

import matplotlib.pyplot as plt
plt.scatter(train_input,train_target,c="blue",label = "train")
plt.scatter(50,knr.predict([[50]]),c="red",label = "pred")
plt.scatter(train_input[indexes],train_target[indexes],c="green",label = "neighbor")
plt.xlabel("length")
plt.ylabel("weight")
plt.legend()
plt.show()

○ 길이가 100 일때 위와 똑같은 과정 수행

knr.predict([[100]])
dist , indexes = knr.kneighbors([[100]])
plt.scatter(train_input,train_target,c="blue",label = "train")
plt.scatter(100,knr.predict([[100]]),c="red",label = "pred")
plt.scatter(train_input[indexes],train_target[indexes],c="green",label = "neighbor")
plt.xlabel("length")
plt.ylabel("weight")
plt.legend()
plt.show()

▶ KNN 최근접이웃모델의 특성상 기준 데이터보다 상당히 큰 값의 독립변수가 나와도 가장 가까운 이웃을 이용하여 종속변수 값이 예측되기 때문에 길이가 50일때와 100일때의 무게값이 동일하게 나온다.

-> KNN 최근접이웃모델의 한계

< KNN의 한계 >

- 가장 가까운 이웃을 이용해서 예측을 수행하는 모델이기에 예측하고자 하는 독립변수의 값이 기존 훈련 데이터의 독립변수가 가지고 있는 범위를 벗어나는 경우에는 값이 항상 동일하게 나옴(가까운 거리의 이웃이 항상 동일해짐)

- 따라서 다른 회귀모델을 사용해야함

< 회귀모델 종류 >

- 선형회귀모델(하나의 직선) , 다항회귀모델(곡선) , 다중회귀모델(여러개의 직선) , 릿지 , 라쏘 ,

랜덤포레스트 , 그래디언트부스트 , 히스토그램그레이디언트 부스트 , XGBoost , 기타 등등

- 주로 많이 사용되는 회귀모델 : 릿지 , 히스토그램그레디언트부스트 , XGBoost

- XGBoost는 sckit learn 에 포함되지 않은 별도 라이브러리

- 회귀와 분류 모두 사용가능 : 랜덤포레스트 , 그래디언트부스트 , 히스토그램그레이디언트 부스트 , XGBoost

- 튜닝을 하면서 훈련 가능 - 성능 높이는 용도 : 릿지 , 라쏘

2. 선형회귀모델(LR - Liner Regression Model)

① 라이브러리 불러들이기

from sklearn.linear_model import LinearRegression

② 모델 생성 & 훈련

-> 지도학습

lr = LinearRegression()
lr.fit(train_input , train_target)

③ 훈련/테스트 정확도 확인하기

# 훈련 정확도 확인하기
train_r2 = lr.score(train_input,train_target)
# 테스트 정확도
test_r2 = lr.score(test_input,test_target)
print(f"{train_r2} / {test_r2}")

0.9398463339976041 / 0.824750312331356

▶ [해석]

- 결정계수 확인 결과, 훈련 결정계수 > 테스트 결정계수 이기에 과소적합은 일어나지 않았음

- 두 계수의 차이가 0.12로 과대적합이 의심됨(0.1 이상이면 의심)

④ 임의 데이터로 예측하기

lr.predict([[50]])

1241.838603

▶ KNN에서는 1033g을 예측했었음 이전 보다 증가한 것으로 보아 신빙성이 있어보임

⑤ 추세선(예측선) 그리기

○ 추세선 그리기 위한 계수값 y절편 추출하기

- 직선의 방정식 y = a * x + b

- coef_ : 기울기(계수) -> a

- intercept_ : y절편 -> b

lr.coef_,lr.intercept_

(array([39.01714496]), -709.0186449535474)

○ 추세선 그리기 ( 15 , 50 )

# 훈련데이터 산점도
plt.scatter(train_input,train_target)
# 예측값 산점도
plt.scatter(50,lr.predict([[50]]), marker = "^" , c = "red")
# 추세선 
plt.plot([15 , 50], [lr.coef_ * 15 + lr.intercept_ , 
                     lr.coef_*50 + lr.intercept_] , c = "green")
plt.grid()
plt.xlabel("length")
plt.ylabel("weight")
plt.show()

▶ 추세선에서 산점도의 점까지의 거리가 mae

○ 추세선 그리기 ( 0 , 50 )

# 훈련데이터 산점도
plt.scatter(train_input,train_target)
# 예측값 산점도
plt.scatter(50,lr.predict([[50]]), marker = "^" , c = "red")
# 추세선 
plt.plot([0 , 50], [lr.coef_ * 0 + lr.intercept_ ,
                     lr.coef_*50 + lr.intercept_] , c = "green")
plt.grid()
plt.xlabel("length")
plt.ylabel("weight")
plt.show()

▶ [해석]

- 임의 값 예측 시 KNN 보다는 성능이 좋은 예측이 가능하며 과적합이 발생하지 않는 일반화된 모델로 보여진다.

- 그러나 y 절편의 값이 음수로, 예측 시 음수의 데이터가 예측 될 가능성이 있는 모델로 보여진다.

- 종속변수 무게의 값은 0 이하로 나올 수 없기에 이상치를 예출할 수 있는 모델로 현재 사용하는 데이터를 예측하기에는 부적합한 모델로 여겨진다.

3. 다항회귀모델

< 다항회귀모델 >

- 데이터의 분포가 선형이면서 곡선을 띄는 경우에 사용됨

- 곡선(포물선)의 방정식이 적용되어 있음

- y = (a * x^2 ) + (b * x) + c

- 독립변수는 2개가 사용됨 : x^2 값과 x 값

① 훈련 및 테스트 데이터의 독립변수에 x^2값 추가하기

# 훈련 독립변수
train_poly = np.column_stack((train_input**2 , train_input))
# 테스트 독립변수
test_poly = np.column_stack((test_input**2 , test_input))
print(train_poly.shape , test_poly.shape)

(42, 2) (14, 2)

② 모델 생성 및 훈련 & 과적합 여부 확인

- 선형 , 다항 , 다중 회귀모델은 하나의 모델(클래스) 사용

- 직선 , 곡선에 대한 구분은 독립변수의 개수로 모델이 알아서 구분해준다.

lr = LinearRegression()
lr.fit(train_poly , train_target)
train_r2 = lr.score(train_poly,train_target)
test_r2 = lr.score(test_poly,test_target)
print(train_r2, test_r2)

0.9706807451768623 0.9775935108325122

▶ 훈련 < 테스트 이므로 과소적합에 해당함.(0.007 정도 차이)

③ 임의의 데이터 예측하기

길이가 50 일때

lr.predict([[50**2 , 50]])

1573.984235

④ 추세선을 위한 계수와 y절편 구하기

lr.coef_ , lr.intercept_

(array([ 1.01433211, -21.55792498]), 116.0502107827827)

a = lr.coef_[0]
b = lr.coef_[1]
c = lr.intercept_
print(a , b , c)

1.0143321093767301 -21.557924978837352 116.0502107827827

⑤ 추세선 그리기

plt.scatter(train_input,train_target)
plt.scatter(50,lr.predict([[50**2 , 50]]), marker = "^" , c = "red")
# 추세선
# 추세선이 사용할 x축값 지정(0~50까지의 순차적인 값 사용)
point = np.arange(0,51)
plt.plot(point,a*point**2 + b*point + c , c="green")

plt.grid()
plt.xlabel("length")
plt.ylabel("weight")
plt.show()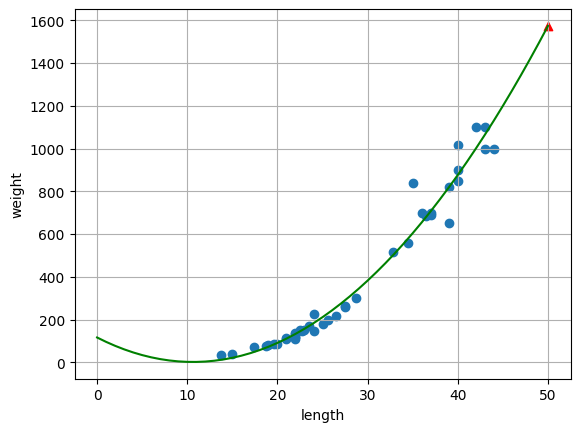

▶ [해석]

나의 해석

- 선형 회귀모델의 추세선과 비교하였을때 다항회귀모델의 곡선 그래프가 훈련 데이터의 값들과의 거리 차이

즉 오차가 적다는 것을 알 수 있다.

- 그러나 길이가 10보다 작은 경우에는 길이가 작아짐에 따라 무게가 줄어들지 않고 증가하는 추세를 보여

이상치가 예출될 수 있으리라 예상된다.

강사님 해석

- 선형회귀모델의 경우에는 음의 절편값이 나타나는 모델이었으나 다항회귀모델의 경우에는 이를 해소할 수 있었다.

- 다항 회귀모델의 훈련 및 테스트 결정계수의 결과 미세한 과소적합을 보이고 있으나 사용가능한 모델로 판단된다.

- 선형회귀모델에 비하여 전체적으로 추세선에 가깝게 위치하고 있기에 오차가 적은 모델이라고 판단된다.

< 과적합을 해소하기 위한 방법 >

- 데이터 양(row 데이터 , 행)을 늘릴 수 있는지 확인

- 분석 모델이 좀 더 집중해서 훈련할 수 있도록 -> 특성(독립변수)을 추가하는 방법 확인

--> 특성을 추가(늘리는)하는 방법은 "특성공학" 개념을 적용

--> 특성을 늘려서 사용하는 모델로 다중회귀모델이 있음

--> 특성을 늘린다는 의미는 훈련의 복잡도를 증가시킨다고 표현하며 ,

복잡도가 증가되면 훈련의 집중력이 강해지게됨

- 복잡도를 늘리는 방법으로는 규제 방법이 있음

--> 규제를 하는 하이퍼파라메터 속성을 이용하는 방식으로 릿지와 라쏘 회귀모델 방식이 있음

- 이외 다른 회귀 모델을 사용하여 비교

● 특성 ( = 컬럼 , 필드 , 퓨처 ) 모두 같은 의미

- 데이터 처리 분야에서는 컬럼 또는 필드라고 칭함

- 머신러닝에서는 특성이라고 칭함

- 딥러닝에서는 퓨처라고 칭함

4. 다중회귀모델(Multiple Regression)

- 여러개의 특성을 사용한 회귀모델

- 특성이 많을 수록 복잡도가 증가됨(훈련시간이 오래걸림 , 시스템 성능에 따라 빠를 수도 있음)

- 다중회귀모델 공식

1차원 데이터 , x는 최소 3개 이상

y = a * x1 +b * x2 + c * x3 + ... + y절편

< 농어의 길이, 두께, 높이 값을 이용해서 무게 에측하기 >

- 독립변수 : 길이, 두께 , 높이

- 종속변수 : 무게

① 데이터 불러들이기

사용할 데이터프레임 변수 : df

import pandas as pd
df = pd.read_csv('data/03_농어의_길이_높이_두께_데이터.csv')

데이터 프레임 형태로 농어의 길이, 높이 , 두께의

데이터가 총 56개 들어가있다.

② 독립변수 생성하기

- 데이터 프레임의 특성 중에 독립변수로 사용할 특성들을 2차원의 리스트 또는 배열 형태로 만들어야 한다.

perch_full = df.to_numpy()
perch_full

데이터프레임명.to_numpy를 통해

데이터 프레임 형식을 배열형식으로 바꿔줌

③ 종속변수 생성하기(이전 데이터 사용)

import numpy as np
# 농어 무게
perch_weight= np.array(
    [5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0,
     110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0,
     130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0,
     197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0,
     514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0,
     820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0,
     1000.0, 1000.0]
)

▶ 독립변수와 종속변수의 행의 개수는 동일해야한다.

이전 데이터에서 농어 무게를 가져왔다.

④ 훈련 및 테스트 데이터 분류하기

- 분류 기준 : 테스트 데이터를 30%로 , 랜덤규칙은 42번

from sklearn.model_selection import train_test_split
train_input,test_input,train_target,test_target = train_test_split(perch_full,perch_weight,test_size=0.3,random_state=42)
print(f"{train_input.shape}, {train_target.shape}/{test_input.shape} , {test_target.shape}")

(39, 3), (39,)/(17, 3) , (17,)

⑤ 모델 생성 & 훈련 & 정확도 확인

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_input,train_target)
train_r2 = lr.score(train_input,train_target)
test_r2 = lr.score(test_input,test_target)
print(train_r2, test_r2)

0.9537065271284176 / 0.886342083634778

▶ 과적합 여부 판단 : 훈련 > 테스트 이며 0.07 정도 차이나므로 과적합에 해당하지 않는 일반화된 모델

다만 검증(테스트) 정확도가 0.8대에서 0.9대로 올릴 수 없을지 고민해볼 필요성이 있어보임

- 특성공학을 적용하여 특성 늘리는 방법으로 집중도를 강화하는 방식을 사용해서 성능 향상이 되는지 확인

⑥ 테스트 데이터로 예측하기

test_pred = lr.predict(test_input)
test_pred

⑦ 평균절대오차(MAE) 확인하기

from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(test_target,test_pred)
mae

68.5665151464055

5. 특성공학 적용시키기

< 특성을 생성하는 라이브러리 >

- 사용 패키지 : sklearn.preprocessing

- 사용 클래스 : PolynomialFeatures(변환기)

- 사용 함수 : fit(훈련 독립변수에서 생성할 특성의 패턴 찾기) , transform(찾은 패턴으로 생성하기)

- 종속변수는 사용되지 않는다.

① 패키지 정의하기

from sklearn.preprocessing import PolynomialFeatures

② 클래스 생성하기

- 특성을 생성시킬때 y절편값도 생성을 함께 시킨다.

- 특성만 있으면 되기 때문에 y절편은 생성에서 제외시키기 위해 include_bias = False로 설정한다

poly = PolynomialFeatures(include_bias=False)

③ 샘플 데이터로 어떤 특성들이 만들어지는지 확인

# 샘플 데이터
temp_data = [[2,3,4]]
# 특성 만들 패턴 찾기
poly.fit(temp_data)
# 찾은 패턴으로 특성 생성하기
poly.transform(temp_data)

[[ 2. 3. 4. 4. 6. 8. 9. 12. 16.]]

2 ,3, 4 샘플 데이터 기준으로 2^2 , 2*3 , 2*4 / 3^2 , 3*4 / 4^2 의 순서로 패턴이 만들어진다.

④ 실제 독립변수를 이용해서 특성 생성하기

○ 클래스 생성하기

-degree = 2 : 차원을 의미하며 2는 제곱승을 의미함
: 3을 넣으면 2의 제곱, 3의 제곱을 수행
: 4를 넣으면 2의 제곱, 3의 제곱, 4의 제곱승을 수행함
: 기본값은 2 (생략하면 2의 제곱승이 적용됨)

poly = PolynomialFeatures(degree=2 , include_bias=False)

○ 패턴 찾기

- 훈련 독립변수 사용

poly.fit(train_input)

○ 특성 생성하기

# 훈련독립변수에 특성 추가하기
train_poly = poly.transform(train_input)
# 테스트 독립변수에 특성 추가하기
test_poly = poly.transform(test_input)
print(train_poly)

[[ 17.4 4.59 2.94 302.76 79.866 51.156 21.0681 13.4946 8.6436] [ 36. 10.61 6.74 1296. 381.96 242.64 112.5721 71.5114 45.4276] .... ] 과 같은 형태로 만들어짐

train_poly.shape , test_poly.shape

((39, 9), (17, 9))

▶ 특성 개수 동일

○ 사용된 패턴 확인하기

poly.get_feature_names_out()

['x0' 'x1' 'x2' 'x0^2' 'x0 x1' 'x0 x2' 'x1^2' 'x1 x2' 'x2^2']

⑤ 모델 생성 & 훈련 & 정확도 확인 & 평균절대오차 => 해석

lr = LinearRegression()
lr.fit(train_poly,train_target)
train_r2 = lr.score(train_poly,train_target)
test_r2 = lr.score(test_poly,test_target)
test_pred = lr.predict(test_poly)
mae = mean_absolute_error(test_target,test_pred)
train_r2 , test_r2 , mae

(0.9898271546307027, 0.9713771600629656, 30.21688959034275)

▶ [해석]

- 특성공학을 적용하지 않은 모델은 검증(테스트) 정확도가 다소 낮았으며, 오차가 50g 정도 였으나 특성공학을 적용하여 특성을 추가하여 훈련 집중도를 높였을 때는 훈련 및 검증(테스트) 정확도 모두 높아졌으며 과적합이 발생하지 않은 일반화 모델로 오차는 30g 정도의 매우 우수한 모델로 판단됨

- 이 모델을 사용하려면 독립변수의 특성 길이, 높이, 두께 3개의 특성을 사용해야 하며, 특성 생성시 degree2를 적용한 특성을 사용해야함

++ degree = 3으로 하고 위와 같은 코드를 수행했을때

(0.9961910731490242, 0.9454275516669763, 36.615385746919976) 의 값이 나옴

훈련 정확도는 더욱 높아졌지만 오차가 커졌고 훈련 정확도와 검증 정확도의 차이가 크다.

따라서 degree = 2일 때가 더욱 적합한 모델이라고 할 수 있다.

6. 규제

- 과대 또는 과소 적합 중에 주로 과대적합이 발생했을 때 사용된다

- 훈련의 정확도가 다소 낮아지는 경향이 있으나, 검증(테스트) 정확도를 높이는 효과가 있다

- 훈련모델을 일반화하는데 주로 사용되는 방법

- 규제 개념을 적용한 향상된 모델 : 릿지(Ridge)와 라쏘(Lasso)

< 규제 순서 >

1. 정규화(단위(스케일)을 표준화시키는 방식)

2. 규제가 적용된 모델 훈련/검증

① 훈련 및 테스트 독립변수 정규화하기

○ 정규화를 위한 라이브러리

from sklearn.preprocessing import StandardScaler

< 정규화 순서 >

1. 정규화 클래스 생성

2. fit() : 정규화 패턴 찾기 ( 훈련 독립변수 사용 )

3. transform() : 찾은 패턴으로 정규화 데이터로 변환 ( 훈련 및 테스트 독립변수 변환 )

○ 정규화 클래스 생성하기

ss =  StandardScaler()

○ 정규화 패턴 찾기

ss.fit(train_poly)

○ 찾은 패턴으로 훈련 및 테스트 독립변수 변환 생성하기

train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)
print( train_scaled.shape , test_scaled.shape)

(39, 9) (17, 9)

② 릿지(Ridge) 모델

Ridge : 회귀모델 / RidgeClassifier : 분류모델

○ 모델 생성

from sklearn.linear_model import Ridge
ridge = Ridge()

○ 훈련 및 정확도 확인

ridge.fit(train_scaled,train_target)
train_r2 = ridge.score(train_scaled,train_target)
test_r2 = ridge.score(test_scaled,test_target)
train_r2 , test_r2

(0.9849041294689238, 0.9845173591615218)

○ 예측하기 및 평가하기

test_pred = ridge.predict(test_scaled)
mae = mean_absolute_error(test_target,test_pred)
print(train_r2 , test_r2,mae)

0.9849041294689238 0.9845173591615218 29.25391147401825

▶ [해석]

- 과적합 여부를 확인한 결과, 과소적합은 발생하지 않았으며, 기존 특성공학을 적용한 우수한 모델보다

훈련 정확도는 0.005 정도 낮아졌지만 검증(테스트) 정확도는 0.013 높아졌다.

- 또한 평균절대오차(MAE) 도 1g 낮아졌다.

- 따라서 일반화되고 오차가 작은 Ridge(릿지) 모델은 매우 우수한 모델로 판단된다.

③ 라쏘(Lasso) 모델

- 회귀만 가능

○ 사용할 패키지 정의

from sklearn.linear_model import Lasso

○ 클래스 생성 ~ 평가하기 - 위와 동일하게 진행

lasso = Lasso()
lasso.fit(train_scaled,train_target)
train_r2 = lasso.score(train_scaled,train_target)
test_r2 = lasso.score(test_scaled,test_target)
test_pred = lasso.predict(test_scaled)
mae = mean_absolute_error(test_target,test_pred)
print(train_r2,test_r2,mae)

0.9861305259897015 0.9863220281055399 26.878384450173456

▶ [해석]

- 0.0002 정도의 과소적합이 있는 것으로 보임

- 오차값도 3g 정도 작아 졌음

- 과소적합이 미세한 차이이기 때문에 릿지 모델과 비교 했을 때 나쁜 모델은 아니지만 사용하기에는 미흡한 부분으로 판단됨

④ 하이퍼파라메터 튜닝하기(규제적용)

○ 릿지 모델 규제 튜닝하기

- alpha : 규제강도 값

- 값의 범위 0.001 ~ 100 사이의 값

- 값이 작을수록(규제강화) 훈련 정확도는 낮아지면서, 과적합에 도움을 주게됨 (가장 좋은것 기준으로 값 작음/큼)

- 값이 커질수록(규제완화) 훈련 정확도는 높아짐, 과적합에는 도움이 되지 않을 수도 있음

- 기본값은 1

ridge = Ridge(alpha=1)
ridge.fit(train_scaled,train_target)
ridge.score(train_scaled,train_target),ridge.score(test_scaled,test_target)

(0.9849041294689238, 0.9845173591615218)

# 1 : (0.9849041294689238, 0.9845173591615218)
# 0.1 :(0.9882780161390031, 0.9868237771849515)
# 0.01 :(0.9887392788057466, 0.9851828913418644)
# 0.001 : (0.9891665643761298, 0.9844479791505648)
# 10 : (0.9763709669744302, 0.9685232855611061)
# 0.15 : (0.9881170058246855, 0.9873558619707502)

가장 좋은 것 : 0.1

○ 라쏘 모델 규제 튜닝하기

lasso = Lasso(alpha=0.1)
lasso.fit(train_scaled,train_target)
lasso.score(train_scaled,train_target),lasso.score(test_scaled,test_target)

(0.9883448062768178, 0.9857016019582314)

▶ 릿지와 라쏘 비교해보니 릿지 모델이 더욱 우수함(일반화되고 훈련정확도가 높으면서 오차가 적음)

728x90