[시계열분석] Prophet , Arima Model
Best Model을 이용해서 잔차 확인
* 잔차 : 실제값과 예측값과의 차이
* 잔차 검정 : 정상성, 정규성 등을 만족하는지 확인하는 검정
* 검정하는 함수 : summary(), plot_dignstics()
○ summary()
model.summary()<class 'statsmodels.iolib.summary.Summary'>
"""
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 2517
Model: SARIMAX(1, 1, 0) Log Likelihood -4108.843
Date: Tue, 16 Jan 2024 AIC 8221.686
Time: 09:18:25 BIC 8233.347
Sample: 0 HQIC 8225.918
- 2517
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.0677 0.011 -6.070 0.000 -0.090 -0.046
sigma2 1.5346 0.018 87.291 0.000 1.500 1.569
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 10915.24
Prob(Q): 0.98 Prob(JB): 0.00
Heteroskedasticity (H): 20.60 Skew: -0.15
Prob(H) (two-sided): 0.00 Kurtosis: 13.20
===================================================================================
▶ P>|z| : p-value
Heteroskedasticity (H) 값이 클 수록 정규 분포, 일반적으로 100 기준 , 20은 작은편
model.plot_diagnostics(figsize=(16,8))
plt.show()
▶ 좌상단 : 잔차 그래프 -> 정상성확인
우상단 : 초록색이 해당 데이터가 정규성 띄는 정도
좌하단 : 분위 시각화, 빨간선이 파란색 실제 값이 걸쳐져있다면 정규성을 띈다고함
우하단 : 정상성 띄는 그래프, 차수 하나(제일 앞에 0) 값만 빼고 정상성 띔
>> 전체적으로 정상성은 띄고 있으나 정규성은 조금 낮음
>> 훈련이 가능함
◇ ARIMA 모델 훈련 및 테스트하기
○ 훈련 및 테스트 데이터 9:1로 분리
- 시계열 데이터는 train_test_split 함수를 사용하지 않는다
-> 연속성을 띄는 데이터의 특성상 데이터를 앞/뒤의 비율로 분리한다
# 훈련 및 테스트 데이터 9:1로 분리
n = int(len(data)*0.9)
train_data = data[:n]
test_data = data[n:]
train_data.shape , test_data.shape((2265,), (252,))
○ auto_arima 모델 설정 및 Best Model 추출
- auto_arima는 훈련과 동시에 베스트 모델을 생성해준다.
model_fit = pm.auto_arima(
y=train_data,
d=n_diffs,
start_p=0,max_p=3,
start_q=0,max_q=3,
m=1,seasonal=False,
stepwise=True,
trace=True
)Performing stepwise search to minimize aic
ARIMA(0,1,0)(0,0,0)[0] intercept : AIC=6127.619, Time=0.13 sec
ARIMA(1,1,0)(0,0,0)[0] intercept : AIC=6119.112, Time=0.08 sec
ARIMA(0,1,1)(0,0,0)[0] intercept : AIC=6119.471, Time=0.12 sec
ARIMA(0,1,0)(0,0,0)[0] : AIC=6134.024, Time=0.03 sec
ARIMA(2,1,0)(0,0,0)[0] intercept : AIC=6120.306, Time=0.11 sec
ARIMA(1,1,1)(0,0,0)[0] intercept : AIC=6118.765, Time=0.28 sec
ARIMA(2,1,1)(0,0,0)[0] intercept : AIC=6120.763, Time=0.43 sec
ARIMA(1,1,2)(0,0,0)[0] intercept : AIC=6120.763, Time=0.54 sec
ARIMA(0,1,2)(0,0,0)[0] intercept : AIC=6120.804, Time=0.16 sec
ARIMA(2,1,2)(0,0,0)[0] intercept : AIC=6120.503, Time=0.91 sec
ARIMA(1,1,1)(0,0,0)[0] : AIC=6126.014, Time=0.13 sec
Best model: ARIMA(1,1,1)(0,0,0)[0] intercept
Total fit time: 2.911 seconds
model_fit.summary()<class 'statsmodels.iolib.summary.Summary'>
"""
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 2265
Model: SARIMAX(1, 1, 1) Log Likelihood -3055.382
Date: Tue, 16 Jan 2024 AIC 6118.765
Time: 09:45:16 BIC 6141.664
Sample: 0 HQIC 6127.120
- 2265
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 0.0851 0.028 3.000 0.003 0.030 0.141
ar.L1 -0.4906 0.106 -4.650 0.000 -0.697 -0.284
ma.L1 0.4247 0.108 3.915 0.000 0.212 0.637
sigma2 0.8704 0.011 82.185 0.000 0.850 0.891
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 9707.42
Prob(Q): 0.99 Prob(JB): 0.00
Heteroskedasticity (H): 11.78 Skew: 0.20
Prob(H) (two-sided): 0.00 Kurtosis: 13.14
===================================================================================
▶ ar : 자기상관 , ma : 이동평균 모두 유의미함
전체적으로 정상성을 띄고 있음(p-value < 0.05)
정규성이 더 낮아짐
◇ Best Model을 이용하여 예측(Predict)하기
* 시계열에서 예측 용어 : forecast라고 칭함
* 예측 결과 : 예측 데이터, 상한가(상한바운드), 하한가(하한 바운드)
* 결과 시각화 : 기존값과 예측값이 연결된 시각화
* 수행방법 : forecast 함수 생성 후 predict 수행
: 예측결과 반환
○ 함수 생성하기
# 향후 예측
# - model : Best Model
# - n : 예측하려는 향후 기간(디폴트로 1을 지정했음)
import numpy as np
def forecast_n_step(model, n=1):
# 예측하기
# - n_periods : 예측기간(일 단위)
# - return_conf_int : 신뢰구간 반환여부
# -fc : 예측결과(y_pred)
# - conf_int : 신뢰구간
fc, conf_int = model.predict(n_periods=n, return_conf_int=True)
# 반환값은 리스트 형태로 변환해서 전달
return (
fc.tolist()[0:n],
np.asarray(conf_int).tolist()[0:n]
)# 함수 생성하기
import pandas as pd
def forecast(len, model, index, data=None):
# 결과값을 담아서 반환할 변수
y_pred = []
pred_upper = []
pred_lower = []
# 데이터(data)가 있는 경우
if data is not None:
for new_data in data:
# 예측하기 : 반복수행을 위해 함수로 생성
fc,conf = forecast_n_step(model)
# 예측결과 리스트에 담기
y_pred.append(fc[0])
# 상한가
pred_upper.append(conf[0][1])
# 하한가
pred_lower.append(conf[0][0])
# 시계열에서는 데이터별로 Model을 갱신함
model.update(new_data)
# 데이터(data)가 없는 경우
else:
for i in range(len):
fc,conf = forecast_n_step(model)
# 예측결과 리스트에 담기
y_pred.append(fc[0])
# 상한가
pred_upper.append(conf[0][1])
# 하한가
pred_lower.append(conf[0][0])
# 시계열에서는 데이터별로 Model을 갱신함
model.update(fc[0])
# 결과값에 대해서는 시리즈 타입으로
return pd.Series(y_pred, index=index),pred_upper,pred_lower
○ 함수 호출하기
- fc : 예측 결과
- upper : 상한가
- lower : 하한가
# 함수 호출하기
fc, upper, lower = forecast(len(test_data),model_fit,test_data.index,data=test_data)
fc, upper, lower (Date 2021-10-29 96.297389 2021-11-01 145.438920 2021-11-02 142.084043 2021-11-03 144.516818 2021-11-04 145.914083 ... 2022-10-24 101.439596 2022-10-25 102.866358 2022-10-26 104.757134 2022-10-27 95.317290 2022-10-28 93.072843 Length: 252, dtype: float64,
[99.29352712735168, 149.01772785379077, .... 99.0740541620581, 96.83018979871885],
[93.30124999571525, 100.4363636166964 .... 101.01693316527634, 91.56052488945483, 89.31549601024618])
▶ 예측결과, 상한가 리스트, 하한가 리스트가 출력됨
◇ 상한가와 하한가의 리스트 타입 데이터를 날짜를 인덱스로하는 시리즈 타입으로 변환하기
- 추후 시각화시 결과값의 인덱스와 매핑하여 그리기 위해
lower_series = pd.Series(lower,index=test_data.index)
upper_series = pd.Series(upper,index=test_data.index)
lower_series,upper_series
◇ 전체 시각화
- 훈련데이터, 테스트데이터 시각화
- alpha 값은 투명도
# 훈련데이터, 테스트데이터 시각화
plt.figure(figsize=(20,6)
)
plt.title("시계열 분석 결과 시각화")
# 훈련데이터
plt.plot(train_data,label="train data")
# 테스트데이터
plt.plot(test_data,label="test data(예측 전 실제값)",c='b')
# 테스트데이터로 예측한 결과
plt.plot(fc,label="예측결과",c='r')
# 상한가(상한바운드) 하한가(하한바운드) 그리기
plt.fill_between(lower_series.index,lower_series,upper_series,alpha=.8,color="k")
plt.legend()
plt.show()

◇ 모델 성능 평가
○ 라이브러리 정의
from sklearn.metrics import mean_squared_error,mean_absolute_error
import math
○ 평균제곱오차 (MSE)
- np.exp : 소수점 형태로 나타내기
mse = mean_squared_error(np.exp(test_data),np.exp(fc))
mse4.220020683466661e+128
○ 평균절대오차 (MAE)
mae = mean_absolute_error(np.exp(test_data),np.exp(fc))
mae4.104694952552019e+63
▶ 평균제곱오차와 평균절대 오차가 낮을 수록 좋은 성능의 모델이라 판단할 수 있음
○ RMSE(Root Mean Squared Error)
- 예측값과 실제값 간의 거리를 나타내는 지표
- 값이 작을 수록 모델의 성능이 좋다고 해석
rmse = math.sqrt(mean_squared_error(np.exp(test_data),np.exp(fc)))
# rmse = math.sqrt(mean_squared_error(test_data,fc))
rmse2.0542688926882627e+64
○ MAPE(Mean Absolute Percentage Error)
- 예측값과 실제값간의 백분율 오차 평균
mape = np.mean(np.abs(np.exp(fc) - np.exp(test_data)) / np.abs(np.exp(test_data)))
mape*10010722.982861409768
▶ 10722% 의 오차가 발생했다는 의미
◇ 한국 증권거래소(KRX)의 주식거래일을 기준으로 1년 후 예측하기
○ 사용 라이브러리
- 한국증권거래소(KRX)의 주시거래일자에 대한 데이터 수집을 위한 라이브러리
- 설치 필요 : pip install exchange_calendars
import exchange_calendars as ecals
○ 주식 거래일자 수집하기
# 주식 거래일자 수집하기
# 원본 인덱스의 마지막 인덱스 일자 이후부터 1년치에 대한 거래일자 수집
# 거래 시작일
start = '2022-11-01'
# 거래 종료일
end = '2023-10-31'
# 한국증권거래소(KRX) code 값 : XKRX
k = ecals.get_calendar("XKRX")
# 시작 및 종료 기간 동안의 거래일 정보 가지고오기
df = pd.DataFrame(k.schedule.loc[start:end])
# open 컬럼을 사용
# - open 컬럼을 사용하기위해 날짜 정보를 리스트에 추가하기
date_list = []
for i in df["open"]:
date_list.append(i.strftime("%Y-%m-%d"))
# DatetimeIndex 형태로 변환하기
date_index = pd.DatetimeIndex(date_list)
date_indexDatetimeIndex(['2022-11-01', '2022-11-02', '2022-11-03', '2022-11-04',
'2022-11-07', '2022-11-08', '2022-11-09', '2022-11-10',
'2022-11-11', '2022-11-14',
...
'2023-10-18', '2023-10-19', '2023-10-20', '2023-10-23',
'2023-10-24', '2023-10-25', '2023-10-26', '2023-10-27',
'2023-10-30', '2023-10-31'],
dtype='datetime64[ns]', length=247, freq=None)
▶ 시작일과 종료일 사이의 일자들이 리스트에 들어있는 것을 확인 할 수 있다
○ 1년 후 주가 예측하기
fc2,upper2,lower2 = forecast(len(date_index),model_fit,date_index )
fc2
○ 상한가 하한가 시리즈로 변환하기
lower_series2 = pd.Series(lower2,index=date_index)
upper_series2 = pd.Series(upper2,index=date_index)
lower_series2 , upper_series2
○ 시각화하기
plt.figure(figsize=(20,6))
plt.title("1년뒤 주가 예측")
# 훈련데이터
plt.plot(train_data,label="train data")
# 테스트데이터
plt.plot(test_data,label="test data(예측 전 실제값)",c='b')
plt.plot(fc,label="예측결과",c="r")
# 1년후 주가 예측
plt.plot(fc2,label="1년 후 예측결과")
# 상한가(상한바운드) 하한가(하한바운드) 그리기
plt.fill_between(lower_series.index,lower_series,upper_series,alpha=.9,color="k")
# 1년후예측 - 상한가(상한바운드) 하한가(하한바운드) 그리기
plt.fill_between(lower_series2.index,lower_series2,upper_series2,alpha=0.9,color="k")
plt.legend(loc="upper left")
plt.show()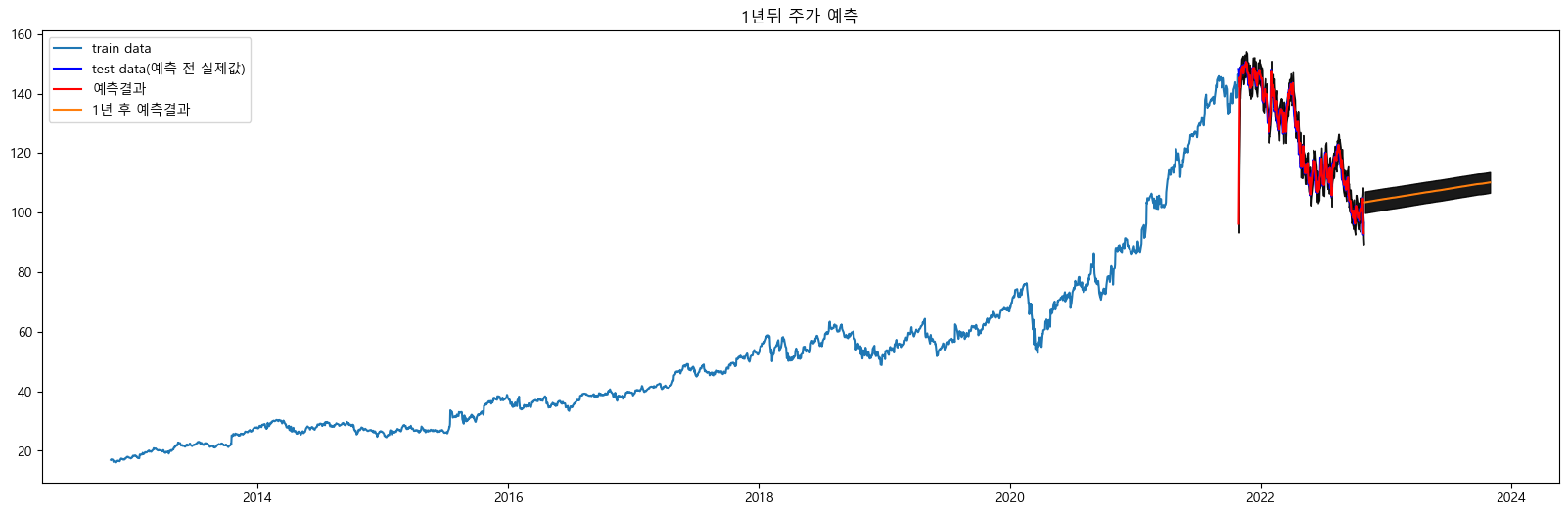
페이스북 시계열 분석 라이브러리 Prophet
* 시계열 예측을 그래프(시각화)로 표현하는 모델
* Prophet 모델에 넣어줘야하는 데이터 형태
- index는 날짜, Date컬럼, Adj Close(수정종가) 컬럼
- Prophet에서 사용하는 컬럼명은 ds, y 컬럼명을 사용
-> 기존 컬럼명을 수정해야함
-> Date 컬럼명은 ds로, Adj Close 컬럼명은 y로 수정
◇ 데이터 전처리
goog_data 사용하여 prophet_data 생성
prophet_data = goog_data.copy()
prophet_data
- Date index는 컬럼 데이터로 변환
- 훈련에 사용할 컬럼명 : Date, Adj Close
- 훈련에 사용하지 않는 컬럼은 삭제
- 훈련에 사용할 컬럼명 변경 : Date -> ds , Adj Close -> y
prophet_data["Date"] = prophet_data.index
prophet_data = prophet_data.reset_index(drop = True)
prophet_data.drop(["Open","High","Low","Close","Volume"],axis=1,inplace = True)
prophet_data.columns = ["y","ds"]
prophet_data
prophet_data.reset_index(inplace=True)
prophet_data.drop(["Open","High","Low","Close","Volume"],axis=1,inplace = True)
prophet_data.columns = ["ds","y"]
prophet_data▶ 강사님 풀이 -> reset_index를 통해 인덱스에 있던 데이터가 컬럼으로 옮겨지는 것도
동시에 수행된다
◇ Prophet 라이브러리 설치
- 가상환경 새로 만들어서 진행 : 버전 충돌이 많이 일어남
- 가상환경 생성 시 python 버전은 3.6버전 사용 (3.9 이하 버전으로 사용)
- Prophet 라이브러리는 C++ 프로그램으로 만들어져 있음
○ Prophet 가상환경 생성 및 라이브러리 설치하기
- 가상환경 생성은 Base에서 명령 실행
- 가상환경 생성 후에는 생성된 가상환경 이름으로 활성화(activate)
- 라이브러리 설치는 생성한 가상환경 안에서 모두 설치 진행
1. 가상환경 신규 생성하기
-> Prophet은 파이썬 3.9 이하 버전에서만 작동함
conda create -n gj_env_prophet python=3.6
2. 생성한 가상환경으로 활성화하기
conda activate gj_env_prophet
3. C++ 라이브러리 설치
- Prophet 은 C++로 만들어진 라이브러리
conda install libpython m2w64-toolchain -c msys2
4. 라이브러리 설치하기
pip install ipython jupyter matplotlib pandas xlrd seaborn scikit-learn
pip install openpyxl
pip install convertdate
pip install lunarcalendar
pip install holidays
pip install cython
pip install wheel
pip install pystan
pip install fbprophet
pip install plotly
pip install jupyter notebook
pip install yfinance
pip install statsmodels
pip install pmdarima
pip install exchange_calendars
5. 커널 생성하기
python -m ipykernel install --user --name gj_env_prophet --display-name gj_env_prophet_kernel
6. 커널 설치 확인
jupyter kernelspec list

○ 라이브러리 정의
from fbprophet import Prophet
◇ Prophet 모델 생성 및 훈련
○ ds 컬럼 데이터 타입 날짜형으로 변경하기
prophet_data.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 2517 entries, 0 to 2516
Data columns (total 2 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 y 2517 non-null float64
1 ds 2517 non-null object
dtypes: float64(1), object(1)
memory usage: 39.5+ KB
prophet_data["ds"] = pd.to_datetime(prophet_data["ds"])
prophet_data.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 2517 entries, 0 to 2516
Data columns (total 2 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 y 2517 non-null float64
1 ds 2517 non-null datetime64[ns]
dtypes: datetime64[ns](1), float64(1)
memory usage: 39.5 KB
○ 모델 생성하기
model = Prophet(daily_seasonality=True)
model
○ 모델 학습시키기
model.fit(prophet_data[["ds","y"]].iloc[:-10])
◇ 3년 후 예측하기
# 3년 후 예측하기
# 기존값에 3년 후 일자를 포함해서 추출하기
future = model.make_future_dataframe(periods=365*3)
# 예측하기
forecast = model.predict(future)
# 시각화
model.plot(forecast)
○ 계절성을 나타내는 그래프 시각화
model.plot_components(forecast)